Research

I am broadly interested in diffuse magnetized plasmas, (magneto)hydrodynamic processes and their role in (astro)physical systems, and related computational topics in the area of high performance computing, large scale simulations, and performance portability. The (current) research questions generally fall into the following categories:

Energy transfer in compressible MHD turbulence

Energy transfer is traditionally (i.e., in the incompressible hydrodynamic regime) expected to happen down-scale, i.e., from large scales to small scales (see also the turbulent cascade below). In magnetohydrodynamics the picture is more complex as two reservoirs of energy exist: kinetic and magnetic energy. Energy injected into one reservoir is not “simply” transferred down-scale any more, but energy exchange between reservoirs (and scales) takes places due to the nonlinear nature of the underlying equations. This process is getting even more complex when compressibility effects are taken into account as additional ways to exchange energy are introduced.

Several studies in the past analyzed the complex nature of energy transfer in the incompressible MHD regime. We are interested in systems where compressible effects, e.g., shock fronts (from galaxy mergers in galaxy clusters), potentially are an important factor within the overall dynamics. For this reason, we have extended established analysis techniques to the compressible regime. The resulting framework has been published and the code is publicly available on GitHub at pgrete:energy-transfer-analysis. Eventually, this analysis allows us to quantify the compressibility effects in different regimes and supports the development of appropriate subgrid-scale models.

We also used the framework to quantify the effect of magnetic tension on the kinetic energy spectrum in driven, magnetized turbulence, see Grete et al. ApJ (2021). Our key finding is that the kinetic energy spectrum develops a scaling of approximately k^−4/3 as the kinetic energy cascade is suppressed by magnetic tension.

More recently, we used the framework to study simulations of stationary MHD turbulence with varying dynamical range, i.e., varying Reynolds numbers. In the context of simulation with implicit/numerical dissipation this simply corresponds to increasing the number of cells (resolution) and keep all other simulation parameter identical. One of the key results of that study is that cross-scale energy fluxes (i.e., the amount of energy transferred from larger to smaller scales) varies both with dynamical range and with different mediators (such as the kinetic energy cascade or magnetic tension). Moreover, did not observe any indication of convergence calling into question whether an asymptotic regime in MHD turbulence exists, and, if so, what it looks like, see Grete et al. ApJL (2023) for more details.

Subgrid-scale modeling of MHD turbulence

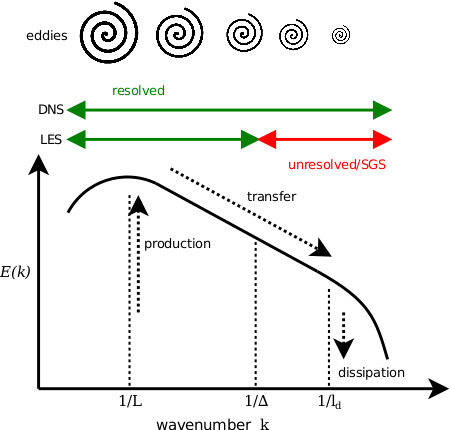
Phenomenologically (incompressible hydrodynamic) turbulence is often described by the successive break-up of large eddies into smaller and smaller eddies. In this picture, the system is driven on largest scales, where energy is injected into the system. This energy then cascades down to smaller scales by inertial motions until it eventually dissipates. Even in moderate systems the separation of scales (between the largest and smallest scales) can already be quite large. In astrophysical system this separation easily spans many orders of magnitudes. The resulting dynamical range is beyond what can be reasonably simulated directly - even on the most powerful supercomputers.

One concept to circumvent this problem is a large eddy simulation (LES). In an LES only the largest scales are simulated directly. The smallest scales are unresolved, in particular, the scales smaller than the grid scale (or below the resolution limit \(1/\Delta\)). However, they can be reintroduced to the simulation by means of a subgrid-scale (SGS) model, which only depends on the quantities that are resolved in the simulation.

While the subject of SGS modeling is well established in the incompressible hydrodynamic regime, there is comparatively little research in the compressible magnetohydrodynamic regime. Given that the latter regime is relevant for astrophysics, e.g., in the interstellar medium, we are working on developing new SGS models that are particularly capable of capturing compressibility effects. Our latest nonlinear model has proven itself to yield better results than traditional models, e.g., eddy-viscosity or scale-similarity type models, in both a priori tests and a posteriori tests.

Driving mechanisms in astrophysical systems

Driving, i.e., energy and momentum input, is ubiquitous in astrophysical systems and comes in many different forms such as feedback from supernovae or from galaxy mergers. One important open question concerns the influence of driving mechanisms on the statistical properties of turbulence. Often statistical properties can be observed directly, e.g., the extent of non-Gaussian statistics of the velocity field in the interstellar medium, and thus are used to deduce physical properties of astrophysical systems. Previous studies already analyzed in detail the influence of the ratio between compressive and solenoidal modes in the driving mechanism. Less attention has been paid to the autocorrelation time of the forcing, i.e., the timescale on which the driving mechanism evolves. We are working on understanding and quantifying physically realistic driving mechanisms, i.e., ones that evolve on a finite timescale within the system. Based on numerical simulations in different regimes and with different driving parameters we were able to show that \( \delta \)-in-time (i.e., uncorrelated in time) driving leads to an artificial injection of compressive modes to the simulation, see Grete et al. ApJL (2018). These artificial compressive modes result in biases in observables such as rotation measures.

Turbulent magnetic fields in the early Universe

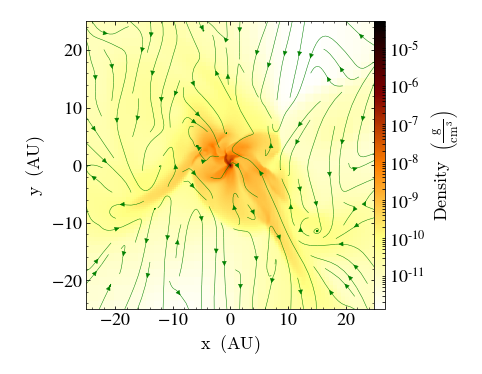Supermassive black holes (SMBHs) with (10⁹) solar masses have been observed in the early Universe at redshifts (z>6). The early formation of such massive objects is still poorly understood and different scenarios are currently being investigated. We are studying direct collapse scenarios with particular emphasis on the influence of turbulent magnetic fields. We do so by running cosmological simulations with Enzo that employ the novel nonlinear subgrid-scale model for MHD turbulence described above. While differences in the stability of accretion disks and their fragmentation are expected due to magnetic torques and angular momentum transport by unresolved magnetic fields, first results indicate that overall the self-similar collapse is the dominant process in determining the properties within the halo, see Grete et al. MNRAS (2019). Fragmentation during the collapse is intermittent and the mass accretion rates of 0.2 to 3 solar masses per year are high enough to make the direct collapse a viable scenario for the formation of SMBH seeds.

More recently, we expanded the setup by also varying the Lyman-Werner radiation background, which impacts the relevant cooling regime (atomic and molecular hydrogen cooling). Again, we find that the small scale dynamo operates over a large range of conditions in the collapsing gas, see Diaz et al. A&A (2024) for more details.

Numerical methods

In relying on simulations to study processes that are otherwise difficult to observe (in experiments or in nature), for example MHD turbulence, it is important to understand the potential impact of the numerical method on the results.

We work with different codes, e.g., Enzo, Athena, or Athena++/K-Athena and conduct simulations under (almost) identical conditions. This allows us to quantify the effects of different numerical methods and their implementations in practice.

Recently, we showed how the energy transfer analysis framework (see Section above) can be used to measure the effective numerical dissipation (particularly viscosity and resistivity) in simulations of stationary MHD turbulence, see Grete et al. ApJL (2023) for details. This also includes a demonstration that implicit large eddy simulations (ILES) match direct numerical simulation (DNS) with the same (effective) transport coefficients.

Performance portability and exascale computing

We are preparing the transition to next generation, exascale systems. While the final architecture and design are still not determined and/or in development, the previous years have shown that the entire environment is quite dynamic, e.g., the cancellation of Intel’s Xeon Phi series, so that performance portability is a key requirement in current code development. Performance portability broadly refers to writing code once that performs well (in the sense of making efficient use of the architecture) on multiple different architectures, e.g., CPUs or GPUs.

We have been exploring Kokkos - a C++ library that abstracts parallel execution and (hierarchical) memory management - Part of this exploration is porting a modern C++ astrophysical MHD code (Athena++) to make use of this approach - eventually allowing us to run the code on large GPU supercomputers.

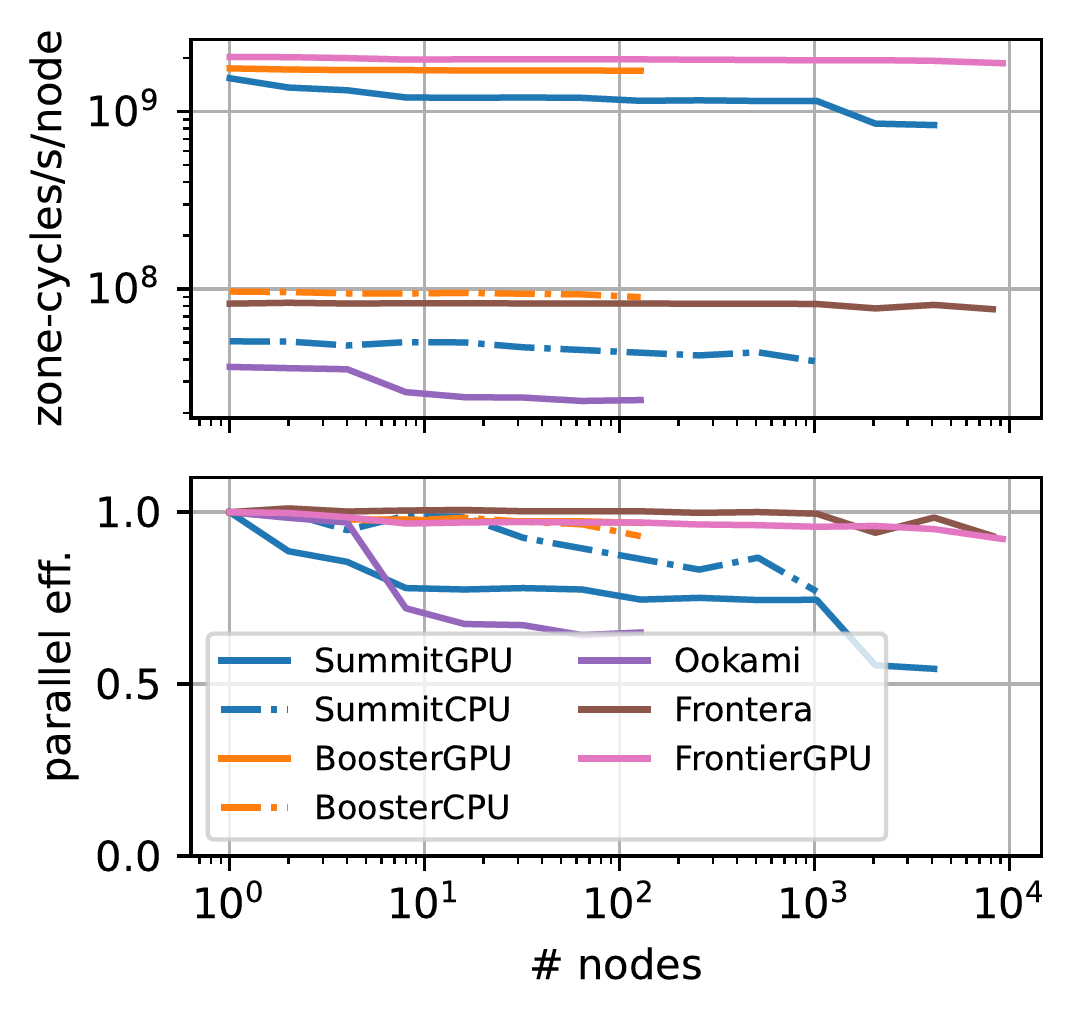
The resulting K-Athena (= Kokkos + Athena++) code is public on GitLab and details regarding the implementation and performance results are reported in an accompanying code paper (Grete et al. 2021). K-Athena achieves about 2 trillion (10¹²) total cell-updates per second for double precision MHD on Summit — the fastest supercomputer in the world at the time. This translates to updating an MHD simulation with a resolution of 10,000³ twice per second! At about 80% parallel efficiency using 24,576 Nvidia V100 Volta GPUs on 4,096 nodes, K-Athena achieves a speedup of more than 30 compared to using all available 172,032 CPU cores.

Based on these results a new collaboration formed to develop a performance portable structured grid adaptive mesh refinement (AMR) framework called Parthenon. The code is now public on GitHub under an open source license and the accompanying code paper has been published (Grete et al. 2022).

Several downstream codes are developed on top of Parthenon including the general relativistic MHD codes Phoebus and KHARMA as well as parthenon-hydro, which is a miniapp solving the compressible Euler equation to illustrate the use of Parthenon in practice, and AthenaPK.

AthenaPK is the successor to K-Athena, i.e., a flexible (M)HD code now with support for performance portable adaptive mesh refinement. First physics application papers have already been published. AthenaPK (and parthenon-hydro) reach 92% weak scaling parallel efficient going from a single node all the way to 9,216 nodes on current TOP500 #1 supercomputer Frontier. At that scale the simulations are running on 73,728 GPUs in parallel. Given their performance the codes are also used in the official OLCF Test Harness that was used for acceptance testing of Frontier as well as for regular performance regression tests at scale.

Generally, we encourage feedback and/or contribution to all codes via their respective repositories.